Optimal Control of Mircogrids
This project explored various control strategies for operating energy microgrids.
Introduction
The project was part of a course project in Optimal Control. The aim was to design a control algorithm to minimise the cost to the user who has a solar installation in a micro-grid that integrates with an external central grid.
The constraints in the system were the variability in the solar input, the variability in the user demand and the presence of a diesel generator to augment the solar and external grid. The aim of the algorithm was to minimise the cost to the user. The principles of optimal control were applied to the problem, and three approaches were taken,
- Forward Euler Method
- Dynamic Programming Method
- Collocation Method
I was part of a team of three consisting of Shashwat Joshi , Arun Venkateswaran and myself.
Model
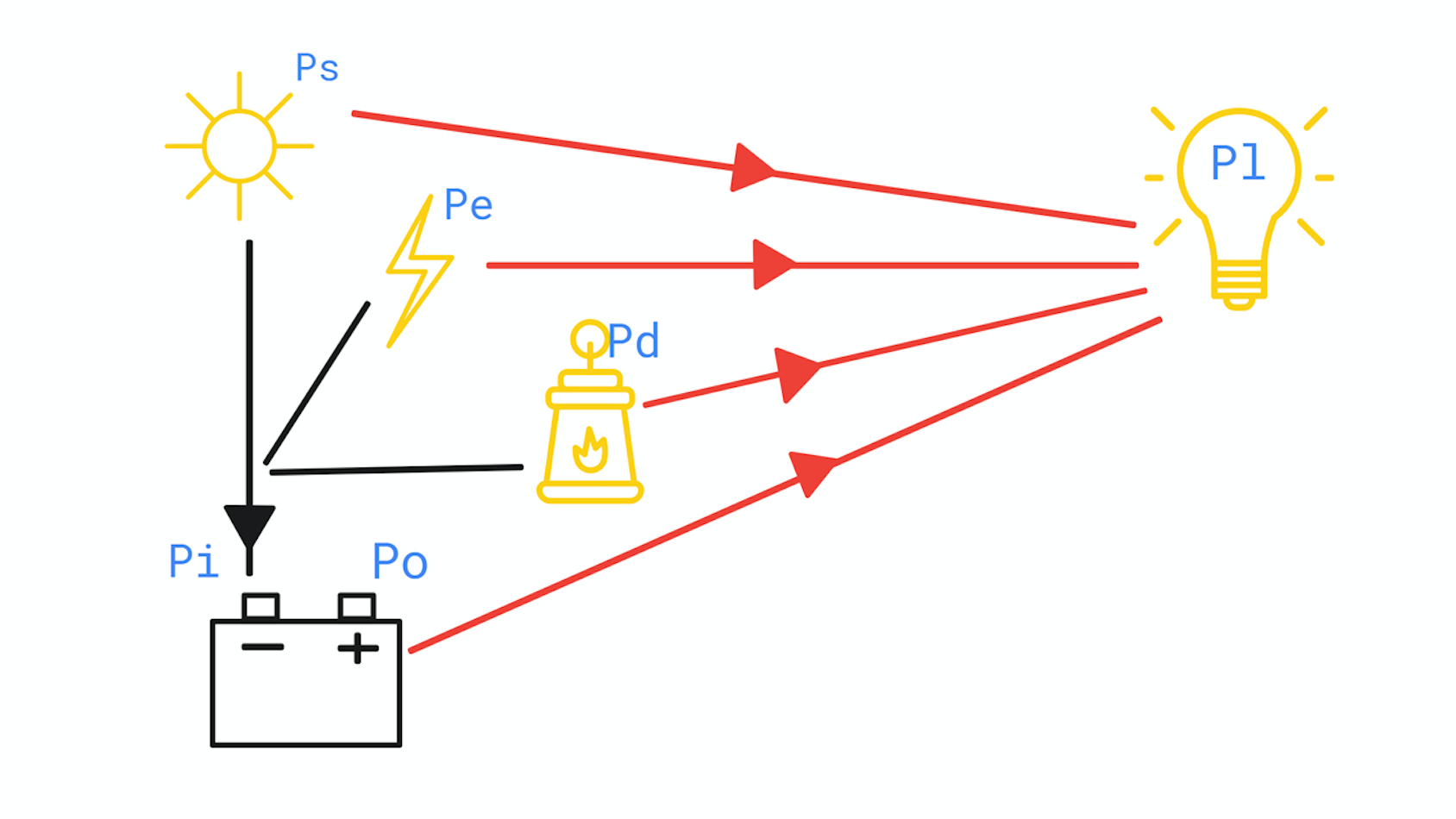
A model of the micro-grid.
The model consists of a solar power supply Ps, external power supply Pe, diesel power Pd, battery input Pi and output Po and the load on the grid Pl.
My Contribution
The three approaches in the project were undertaken by the three of us. I chose the Dynamic Programming approach, which involved creating a Lagrangian scheme for the cost function, and then trying to predict the subsequent states based on the available data.
Apart from this, I was also responsible for conducting the literature review for the project, in which I was able to read the literature of optimal control applied in the domain of micro-grid energy management, and was also able to understand the importance of theories outlined by Daniel Liberzon .
I also compiled the final report in Latex on Overleaf, and also made the final presentation to a panel of professors and their graduate students.
The Outcome
The results of the simulation were:
- Since there is no associated cost with solar power, it is always used when available and sufficient. The remaining energy is first supplied by diesel power and then by the external power source, as the unit cost for diesel power is less than that of the external supply.
- All three methods give approx. same minimum cost for one day’s operation
- The computation time for all the processes was high, though the Collocation method gave the fastest results and the Euler method gave the slowest result. The optimisation was done for only a day’s data, as the computation for the month’s data would have taken a very long time.
